Determinazione degli effetti radiativi degli aerosol atmosferici del Mar Mediterraneo nella regione spettrale infrarossa
←
→
Trascrizione del contenuto della pagina
Se il tuo browser non visualizza correttamente la pagina, ti preghiamo di leggere il contenuto della pagina quaggiù
Determinazione degli effetti radiativi degli
aerosol atmosferici del Mar Mediterraneo
nella regione spettrale infrarossa
Irene Mavilia
Relatore interno: WolfangoPlastino
Relatore esterno: Alcide Giorgio di Sarra
Casaccia, 6 aprile 2011Lampedusa
(estensione ≈ 22 km2)
Picture ISS004E11850, courtesy of Earth Sciences and Image Analysis Laboratory
NASA Johnson Space Center (http://eol.jsc.nasa.gov)Flussi radiativi
alla superficie
Proprietà ottiche
dell’aerosol
Condizioni
meteorologiche e
di copertura
nuvolosa del cielo
LampedusaImportanza…
• Solo un numero molto limitato di studi sono stati dedicati a
determinare l’effetto dell’aerosol nell’intervallo infrarosso.
• Ignorare questi effetti può causare errori nei modelli climatici.
• Il lavoro è stato svolto utilizzando solo dati misurati e non estrapolati
da modelli.
…e difficoltà
• Il trasferimento di flussi radiativi infrarossi è fortemente influenzato
dalle nubi e da temperatura e umidità, la cui variabilità produce una
variazione nel segnale molto maggiore di quella dovuta all’aerosol.
• È necessario avere misure di irradianza e spessore ottico molto
precise e accurate.
• L’effetto è altamente variabile con la composizione e la quantità
dell’aerosol e quindi con il tempo e la regione geografica considerata.Trasferimento radiativo
dI λ = −kλ ρI λ ds
Spessore ottico monocromatico
del mezzo, tra 0 e s1:
s1
τ λ ( s1 ,0) = ∫ kλ ρ ⋅ ds'
0
Caso generale:
dI λ SORGENTE:
= −Iλ + Jλ
dτ λ
• emissione
(flussi terrestri)
• diffusione nella Legge di Beer-Bouguer-Lambert
ESTINZIONE:
• assorbimento
stessa direzione I λ ( s1 ) = I λ (0) exp(−τ λ )
(flussi solari)
• diffusione in altre direzioniAerosol atmosferico
particelle micrometriche e sub micrometriche, solide o liquide, sospese in aria
ORIGINE
• Naturale: particelle provenienti da deserti, spume marine, eruzioni
vulcaniche, incendi boschivi, reazioni chimiche di gas naturali,…
• Antropica: particelle emesse da processi di combustione,
industriali, di inquinamento urbano,…
SUL CLIMA
• Effetto diretto: interazione con la radiazione
• Effetto indiretto: funzione di nuclei di condensazione per acqua o
ghiaccio, modificando le proprietà ottiche, la quantità e l’evoluzione
delle nubiIPCC
IntergovernmentalP
anel on
ClimateChange
"Quarto Rapporto di
Valutazione" (2007)
Forcing radiativo
dovuto all’aerosol:
• negativo
• caratterizzato da una
grande incertezza
Obiettivo: migliorare il
livello di comprensione
scientifica per ridurre
queste incertezzeProprietà ottiche dell’aerosol
s
I λ ( s)
• Spessore ottico τ λ ( s,0) = ∫ kλ ρ ⋅ ds = − ln
(estinzione=diffusione+assorbimento) 0 I λ (0)
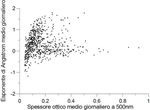
• Esponente di Ångström τ ( λ1 )
ln
τ (λ 2 )
Per l’aerosol: α ≅ [0 ÷ 2] α =− ⇒ τ = τ (1 µ m ) λ − α
λ1
Per le molecole: α ≅ 4 ln
λ2Radiometro MFRSR
(MultifilterRotatingShadowbandRadiometer)
Il radiometro MFRSR misura l’irradianza solare incidente
utilizzando la banda oscurante per separare le componenti globale
(G) e diffusa (D) del campo radiativo, ricavando la componente
diretta (I) dalla sottrazione delle due: I=G-D
1 canale a banda larga ≈(300 ÷ 1000) nm
6 canali centrati a 415.6, 495.7, 614.6, 672.8, 939.6 nm e di ampiezza ≈ 10 nm
Per ogni banda: Vλ = k ⋅ I λ
Legge di Lambert-Beer I λ = I λ 0 exp[−mτ λ ] (τ λ )tot = (τ λ )aerosol+ (τ λ )R + (τ λ )ass
Specie atmosferiche che pesano di più nello
spessore ottico di assorbimento (τ λ ) ass :
• NO2 per la banda a 415.6 nm
• O3 per le bande a 495.7, 614.6, 672,8 nm
• H2O per la banda a 939.6 nm
Misura di contenuto colonnare di vapor d’acquaPirgeometro
Misura irradianza IR (4÷100) µm
verso il basso
L’uscita della termopila è una tensione ΔV proporzionale
alla differenza di temperatura ΔT tra la base e la
sommità della termopila: ∆T = α∆V
Rnet = (Rdn ↓ −Rup ↑) = k∆T Flusso emesso dalla termopila
Flusso trasmesso dalla cupola
Rup ↑= ε 0σ ⋅ TS4
alla superficie della termopila
Porzione del flusso emesso
verso l’alto dalla termopila e
Rdn ↓= Hτ + ε 0 ρσ ⋅ TS4 + εσ ⋅ Td4
riflesso indietro alla termopila
Flusso emesso dalla cupola
alla termopila
Equazione di Calibrazione: [Albrecht and Cox, 1974]
∆V
H= + k 2σTC4 − k3σ (Td4 − TC4 )
sPeriodi e tipologia dei dati
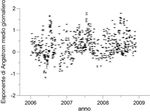
DAL RADIOMETRO MFRSR:
– serie di misure di spessore ottico ai 6 diversi canali e di esponente di
Ångström dal 03/01/2006 al 31/03/2010, campionate ogni 15 secondi
– serie di misure e di contenuto colonnare di vapor d’acqua, dal 3/01/2006
all’1/12/2008, campionate ogni 15 secondi
DAL PIRGEOMETRO:
serie di misure calibrate di irradianza nella regione spettrale (4 ÷ 50) µm, dal
23/03/2006 all’11/03/2010, campionate ogni 30 secondi
DALLA TORRE METEOROLOGICA:
serie di misure di temperatura e umidità relativa dell’aria dall’1/01/2006 al
12/03/2010, campionate ogni 10 minutiAnalisi
• Pulizia manuale dei dati del pirgeometro
• Programmazione con IDL:
– Selezione dei dati nei periodi di cielo sereno
– Unificazione e omogeneizzazione dei dati a 5 minuti
(medie e interpolazioni)
– Classificazione di tre diversi tipi di aerosol
– Selezione delle irradianze in un ristretto intervallo di
temperatura e umidità
– Riduzione dei dati dispersi
– Determinazione dell’efficienza di forcing radiativo
infrarosso dovuto ad ogni tipo di aerosol a LampedusaForcing
Concetto di forcing radiativo diretto (ΔF) dovuto a un agente perturbante come
l’aerosol, relativamente all’intervallo spettrale infrarosso, solare o entrambi.
↓ ↑ ↓ ↑
Alla superficie:
∆F = ( F − F ) − ( F − F )
ca ca sa sa
Si può assumere che l’emissione verso l’alto , pari a ε SσTS , sia la stessa sia in
4
presenza che in assenza di aerosol:
• l’emissività dipende solo dalla caratteristiche della superficie
• la temperatura superficiale del mare varia lentamente
↓ ↓
∆F ≅ F − F ca sa
Differenza tra le irradianze infrarosse verso il
basso: quantità misurate dal pirgeometro
∆F > 0 Riscaldamento della superficie
∆F < 0 Raffreddamento della superficieMETODO DIRETTO:
regressione lineare y=A+Bx
x = spessore ottico a 495.7 nm
y = irradianza infrarossa verso il basso (Wm-2)
Errore totale su x e su y σ tot = σ x2 + σ x2
Deviazione standard della media 1
1 N −1 2
σx = ∑ (x j − x)
2
N ( N − 1) j =0
Errore dominato dall’evoluzione nel
tempo della grandezza fisica x
Propagazione degli errori di misura
1
∑ j (σ x j ) 2
2 Pendenza della retta B:
σx =
N2 ∆F
B= = EFFICIENZA DI FORCING
Errore dominato dagli errori sistematici ∆τ
di calibrazioneSelezione delle misure Considerazioni
di irradianzain statistiche
intervalli ristretti di
temperatura e vapor
T = (26 ÷ 26.5) °C
d’acqua colonnare
T = (17 ÷ 17.5) °C
Ampiezza degli intervalli:
•TEMPERATURA
ΔT=0.5°C
•VAPOR D’ACQUA COLONNARE
ΔCWV=0.25 cm
(CWV = Columnar Water Vapor:
grandezza che tiene conto della quota)ESTATE
(insieme totale dei dati)
T = (26 ÷ 26.5) °C CWV = (2.25 ÷ 2.50) cmPRIMAVERA/AUTUNNO
(insieme totale dei dati)
T = (17 ÷ 17.5) °C CWV = (1.25 ÷ 1.50) cmDifferenti tipi di aerosol a Lampedusa
Tipo di aerosol τ (495,7 nm) α
BU: urbano-da combustione ≥ 0,1 ≥ 1,5
(biomassBurning-Urban/industrial)
DD: desertico (DesertDust) ≥ 0,15 ≤ 0,5
M: misto (Mixed) >0 0,5BU e DD primavera/autunno
BU DD
T=(18 ÷ 18.5)°C e WVC=(0.75 ÷ 1) cm T=(17 ÷ 17.5)°C e WVC=(1.25 ÷ 1.50) cm
B=(-76.8 ± 48.4) Wm-2p-value=0.15>5% B=(43.5 ± 5.7 ) Wm-2 p-valueTOT e M primavera/autunno
TOT M
T=(17 ÷ 17.5)°C e WVC=(1.25 ÷ 1.50) cm T=(16 ÷ 16.5)°C e WVC=(1.25 ÷ 1.50) cm
B=(27.6 ± 3.8 ) Wm-2 p-valueBU e DD estate
BU DD
T=(27 ÷ 27.5)°C e WVC=(1.75 ÷ 2) cm T=(26.5 ÷ 27)°C e WVC=(2.25 ÷ 2.50) cm
B=(-0.8 ± 5.6 ) Wm-2 p-value=0.88>5% B=(39.9 ± 3.1 ) Wm-2 p-valueTOT e M estate
TOT M
T=(26 ÷ 26.5)°C e WVC=(2.25 ÷ 2.50) cm T=(26.5 ÷ 27)°C e WVC=(1.75 ÷ 2) cm
B=(31.9 ± 2.1 ) Wm-2 p-valueContributo percentuale dell’efficienza di
forcing infrarosso
Efficienze di forcing solare
giornaliere (FEd)
Di Biagio et al., JGR, 2009
Tipi di aerosol Efficienze di forcing %infrarossaFEd
infrarosso (Wm-2) (rispetto al totale)
TOT estate 31.9 ± 2.1 24.3 %
DD estate 39.9 ± 3.1 31.9 %
M estate 64.4 ± 6.4 35.2 %
TOT primavera/autunno 27.6 ± 3.8 25.7 %
DD primavera/autunno 43.5 ± 5.7 39.9 %
Efficienza di forcing totale = infrarossa + solareConclusioni • Il lavoro è in sintonia con gli studi che concordano nell’affermare che il raffreddamento della superficie terrestre indotto dall’aerosol nella banda solare può essere parzialmente compensato dall’effetto di riscaldamento nell’infrarosso. • Una migliore determinazione del forcing infrarosso può aiutare a ridurre parte delle incertezze relative agli scenari climatici. • Questo lavoro può considerarsi uno tra i primi studi sull’argomento ed in particolare sull’area del Mar Mediterraneo. • Rappresenta però un primo passo nella ricerca in questo campo e solleva problematiche che aprono la strada a studi futuri. • Possibile sviluppo: considerare il contributo notturno dell’aerosol nell’infrarosso.
GRAZIE
Puoi anche leggere